Indice de réfraction

Cette propriété optique est très importante, en particulier pour le façonnage des gemmes transparentes, qui repose en grande partie sur cette dernière. En effet, si l'on tient compte de l'indice de réfraction, il est possible d'améliorer considérablement leur effet optique.
L'indice de réfraction, constant, dans une certaine mesure, pour une espèce minérale, représente par ailleurs une des caractéristiques essentielles pour l'identification des gemmes. Le principe de la réfraction, qui entraîne la déviation des rayons lumineux au passage de l'air vers un milieu plus dense, l'eau par exemple, est facile à observer.
Une main plongée dans l'eau obliquement paraît pliée. Ce principe est donc connu depuis les temps les plus reculés. Un rayon de lumière atteignant, sous un certain angle, la face d'un cristal, milieu optiquement plus dense que l'air, sera en partie réfléchi (éclat) et en partie réfracté dans le cristal et dévié de sa trajectoire initiale d'un angle bien précis qui est fonction de la valeur de l'inidice de réfraction.
L'angle que défInit la lumière par rapport à la normale à la surface de séparation des milieux est l'angle d'incidence (i) et l'angle qui correspond à la déviation du rayon lumineux dans le milieu de densité différente, l'angle de réfraction (r). On peut distinguer deux cas de réfraction. Soit le rayon passe d'un milieu peu dense - avec indice plus faible - à un milieu optiquement plus dense, et il subira une déviation le rapprochant de la normale à la face de réflexion; soit, au contraire, il passe d'un milieu dense à un milieu moins dense, et il s'éloignera alors de cette normale.
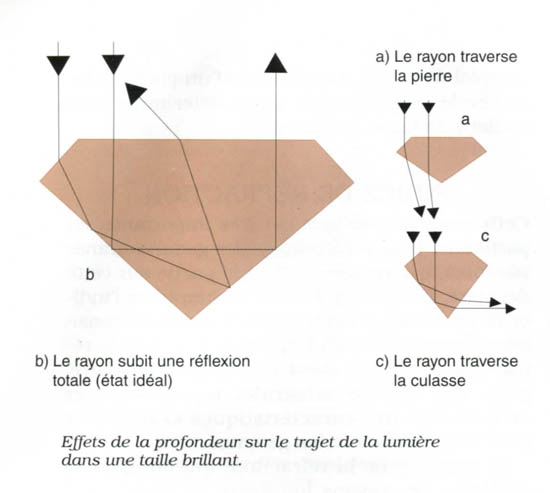
Si l'incidence est verticale, il n'y aura pas de réfraction et le rayon traversera le milieu de densité différente sans être affecté. Lors du passage du rayon lumineux d'un milieu dense vers un milieu moins dense, il peut se produire un autre phénomène, dont on peut tirer profit par le façonnage des gemmes: il s'agit de la réflexion totale du rayon. Cette dernière a lieu systématiquement lorsque l'angle d'incidence dépasse une valeur limite.
Le principe de la réfraction de la lumière est donné par la loi de Snellius (ou loi de Descartes), qui définit le rapport entre l'angle d'incidence et l'angle de réfraction de la manière suivante: sin i/sin r = n (constante). Cette constante a une valeur supérieure à 1 lors du passage d'un rayon passant de l'air, milieu peu dense, vers un milieu optiquement plus dense, comme celui que constitue un minéral. L'indice de réfraction peut être également exprimé sous la forme du rapport des vitesses de propagation du rayon dans l'air M ou dans la gemme (v), ce qui donne la formule suivante: V/v = n.
La vitesse de la lumière dans l'air est d'environ 300 000 km/s. Dans le diamant, elle n'atteint plus que 124 000 km/s.
Avec la formule ci-dessus, on obtient: 300 000/124 000 = 2,42. Cette valeur représente donc l'indice de réfraction du diamant. Il faut savoir également que la valeur de l'angle de réfraction (r) dépend de la longueur d'onde, donc de la couleur de la lumière employée. Plus la longueur d'onde est faible, plus l'angle limite est grand. Pour pouvoir comparer les indices des différentes gemmes, les tableaux indiquant les valeurs sont standardisés pour la lumière monochromatique jaune du sodium (longueur d'onde de 589,3 nm). Il peut y avoir des variations minimes par rapport à cette valeur indiquée, qui sont liées à la couleur propre du minéral.
Pour la plupart des gemmes, les valeurs de base de l'indice de réfraction se situent entre 1,2 et 2,6. On mesure cet indice à l'aide d'un réfractomètre. Un autre moyen, simple, est la méthode d'immersion. Ces différentes méthodes d'identification sont décrites plus en détail dans les ouvrages spécialisés.
La détermination de l'indice de réfraction à l'aide des méthodes indiquées ici offre d'une part l'avantage d'être fiable et relativement précise, et d'autre part de se pratiquer sans dommage pour les gemmes, même lorsqu'elles sont taillées. De plus, elles conviennent également pour des pierres précieuses serties.

Liste Pierres A - J **** Pierres K - Z